Motivated by the graphically interactive program transformation system HOPS, one of my main research interests is higher-order term graph rewriting.
In my dissertation [Kahl-1996], I presented a first algebraic approach to second-order term graph rewriting with the full expressiveness of Combinatory Reduction Systems, thus encompassing lambda calculus. This includes the first algebraic characterisation of graph reduction, an important implementation mechanism for functional programming languages, which before was defined only operationally. The first steps of a generalisation towards relational matching are described in [Kahl-1999d].
For this algebraic characterisation, an extension to the algebraic approach to (graph) rewriting was necessary, yielding a Fibred Approach, also described in more detail in [Kahl-1997b].
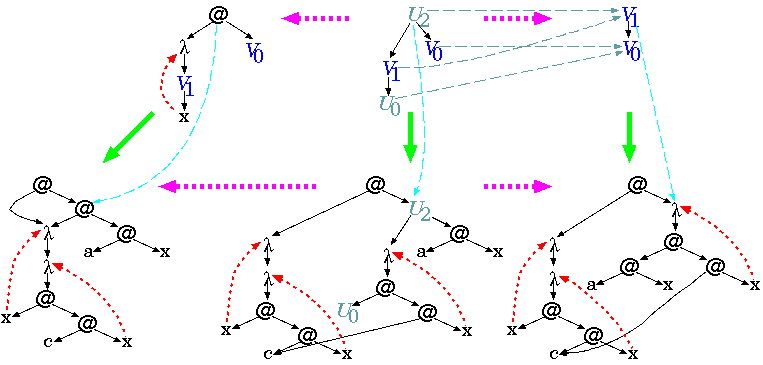
An example application of the rule of beta-reduction applied to term graphs via a fibred rewriting step is shown in the following drawing:

Kinship of fibred rewriting steps with double-pushout rewriting steps is obvious; the main differences are that horizontal morphisms may belong to a different category than vertical morphisms, and that the host object is now the result of a universal construction, thus overcoming the traditional necessity of gluing conditions.
Close inspection of the above rewriting step reveals that sharing is preserved as far as possible, and that the copying of what Wadsworth called ``non-abstractable parts'' already takes places in the construction of the host object, the middle graph of the lower row.
Motivated by HOPS, I have also described an extension of that approach
to typed term graphs
[Kahl-1998d];
the interseting point there is how easily you get access to
advanced typing systems
by considering internally typed term graphs,
with a natural, inference-free ``simultaneous''