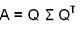
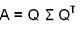
where Q is unitary and is the diagonal singular value matrix. The computation consists of two stages: Lanczos tridiagonalization and symmetric SVD of a symmetric and tridiagonal matrix. This package extends this method to the general case by performing in the first stage a Lanczos bidiagonalization of a general real matrix followed by the SVD of a square bidiagonal real matrix.

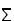
Five Lanczos bidiagonalization functions are provided. The first uses partial orthogonalization, the second uses modified partial orthogonalization and the third uses modified partial orthogonalization with an added restart technique. In general, the modified partial orthogonalization versions are more efficient than the partial orthogonalization version. The modified partial orthoganlization with the restart technique is comparatively more robust. The matrix-vector multiplication in the Lanczos functions can be replaced by a matrix-vector multiplication function to take advantage of the matrix structure. For example, if it is replaced by a fast Hankel matrix-vector multiplication, this package can be used for fast Hankel SVD. Fast Hankel methods are provided for the modified partial orthogonalization and modified partial orthoganlization with restart technique Lanczos methods.

The twisted factorization method for a square bidiagonal real matrix is provided for the second stage of the SVD. The algorithm skips over small subdiagonals in order to maintain numerical stability, potentially resulting in a series of SVDs.

2. Dependency

                                                                                  gFHSVDDemo
                 ______________________________________________________________________|___________________
       _________|_________________                                                     |                   |
      |                    _______|__________________________                     hankelfnrm            appsvd
    gLanPO                |                                  |                                      _______|________
    gLanMPO           gFHLanMPO                         gFHLanMPOR                                 |                |
    gLanMPOR         _____|_____                _____________|______________                   gcstsvdt           clasv2
                    |           |              |             |              |                      |                |
               fhmvmtconv   fhmvmultiply  fhmvmtconv     hankelfnrm    fhmvmultiply             gtwist            slasv2
                                                                                                   |
                                                                                                 gcqds

appsvd.m	SVD of a bidiagonal matrix using twisted factorization, skipping small subdiagonals.
clasv2.m	Compute singular value decomposition of 2x2 upper triangular complex matrix.
fhmvmtconv.m	Converst Hankel matrix to Toeplitz-ciruclant matrix.
fhmvmultiply.m	Fast general Toeplitz-circulant matrix-vector multiplication.
gcqds.m	Compute complex quotient-differences with shift for a general matrix, given Cholesky factorization.
gcstsvdt.m	SVD of an upperbidiagonal matrix using twisted factorization method.
gFHLanMPO.m	General Fast Hankel Lanczos bidiagonalization with modified partial orthogonalization.
gFHLanMPOR.m	General Fast Hankel Lanczos bidiagonalization with modified partial orthogonalization and restart.
gFHSVDDemo.m	Demonstrates general Hankel Lanczos bidiagonalization and SVD.
gLanMPO.m	General Lanczos bidiagonalization with modified partial orthogonalization.
gLanMPOR.m	General Lanczos bidiagonalization with modified partial orthogonalization and restart.
gLanPO.m	General Lanczos bidiagonalization with partial orthogonalization.
gtwist.m	Compute the corresponding eigenvector using twisted factorization.
hankelfnrm.m	Compute the Frobenius norm of an m-by-n, m>=n, Hankel matrix.
slasv2.m	Compute singular value decomposition of a 2-by-2 real upper triangular matrix

• Kevin Browne, Sanzheng Qiao, and Yimin Wei. A Lanczos Bidiagonalization Algorithm for Hankel Matrices. Linear Algebra and Its Applications, to appear, 2008. ( pdf )
  DOI link: http://dx.doi.org/10.1016/j.laa.2008.01.012
• Wei Xu and Sanzheng Qiao, A Twisted Factorization Method for Symmetric SVD of a Complex Symmetric Tridiagonal Matrix, Technical Report No. CAS 06-01-SQ, Department of Computing and Software, McMaster University, Hamilton, Ontario, Canada. L8S 4K1. January 2006. ( ps, pdf )
• F.T. Luk and S. Qiao, A fast singular value algorithm for Hankel matrices, Fast Algorithms for Structured Matrices: Theory and Applications, Contemporary Mathematics 323, Editor V. Olshevsky, American Mathematical Society. 2003. 169--177. ( ps, pdf)

• Download whole package: package.tar
• Download source code of functions:

  appsvd.m	clasv2.m	fhmvmtconv.m	fmvmultiply.m	gcqds.m
  gcstsvdt.m	gFHLanMPO.m	gFHLanMPOR.m	gFHSVDDemo.m	gLanMPO.m
  gLanMPOR.m	gLanPO.m	gtwist.m	hankelfnrm.m	slasv2.m

Professor, Department of Computing and Software
McMaster University, Hamilton, Ontario L8S 4K1, Canada
(905)-5259140 ext 27234