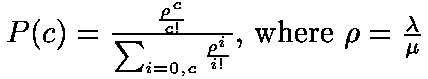
June 1998
In the 1920's, a Danish mathematician and telephone traffic engineer named A. K. Erlang studied delays in telephone traffic and came up with several models which are still in use today. These models deal with the following terms:
The Erlang B model deals with a traffic system in which:
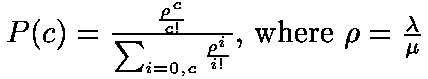
Other common usages include calculating various traffic load statistics such as the maximum service time and the minimum number of phone lines necessary to maintain a given Grade of Service.
Traditional, straightforward evaluation of the given equation results in overflow errors unless rho and c are relatively small (between 100 and 200). To circumvent these problems, we can reformulate the Erlang B formula as:
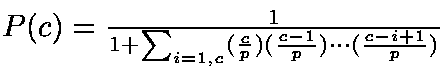
Implementing this rewritten formula efficiently vastly reduces the magnitude of computation, thus allowing larger values for the system. A more detailed discussion of this approach can be found in the companion paper, Qiao and Qiao (1998).
This calculator will handle systems at least as large as rho=1e8,c=1e7, but become prohibitively slow as the systems's magnitude increases. The calculation time becomes noticable when (rho*c) exceeds 10^7. If the calculator's behaviour becomes confusing, clear the fields and try again.