Roadmap
- Concentration Bounds:
- Markov's Inequality
- Chebyshev Inequality
- Chernoff-Hoeffding Bounds
- ...and lots of applications where these are useful!
Concentration bounds
- Key Idea: very often most of the probability is concentrated among small proportion of sample space
- Bound probability that random variable with bell-shaped distribution takes value in tails of the distribution, i.e., far away from the mean.
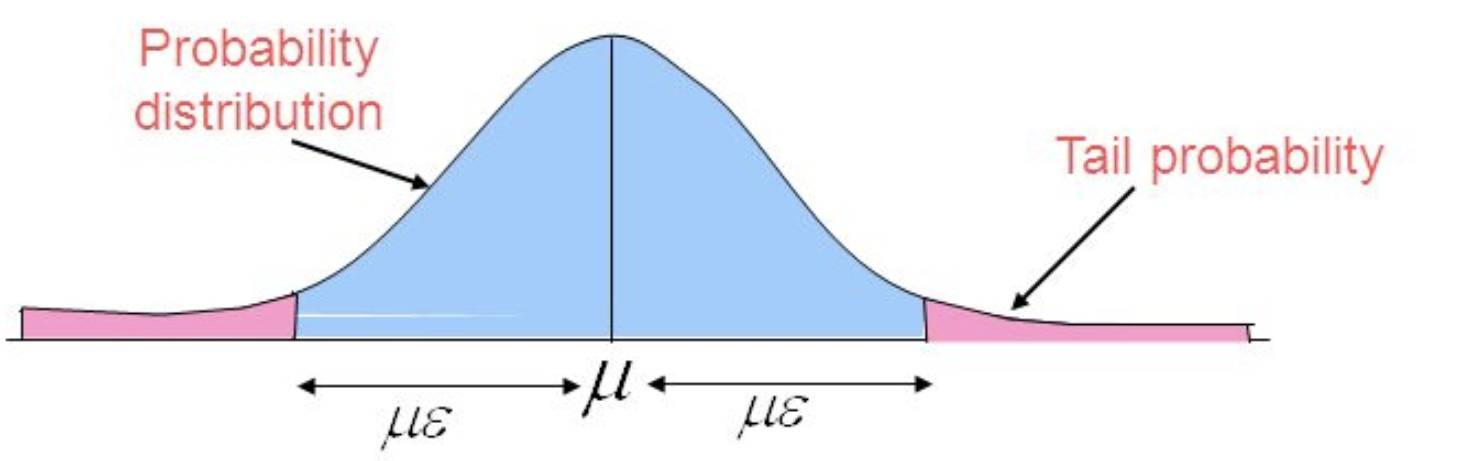
Markov's Inequality
"No more than 1/5 of the population can have more than 5 times the average income."
- The most basic concentration bound
- Requires (almost) no knowledge about properties of random variable
- Consequently, the bound isn't very tight
- Nevertheless many applications
Proof by Picture! :-)
- Define

Proof by Algebra:
Revisiting Distributed MIS Algorithm
- So far, we obtained expected number of rounds.
- Recall:
Idea: Apply Markov's Inequality to RV , since .
- Algorithm terminates within iterations with probability : For , this is
Revisiting Byzantine Agreement
- Let be RV of number of rounds of algorithm.
- To get probability , solve right-hand side for :
Example:
- For :
- For :
Expectation alone might not be Sufficient
Consider the following coin flipping games
- You flip one fair coin. You win $1 if heads; you lose $1 if tails.
- You flip 10 fair coins. You win $1000 if all heads; else you lose $1
Let's compute expected value of winnings :
- Game 1:
- Game 1:
- Which game would you prefer?
Variance
- Red distribution has mean and variance ()
- Blue distribution has mean and variance ()
Example: Variance of Fair Coin Flip
- Let be indicator random variable of fair coin flip. Then:
- .
- .
- What about Variance?
Expectation of Product of Independent RVs
Proof:
Linearity of Variance of Independent RVs
Proof:
- But
- Therefore:
Plan for Today
- Bernoulli & Binomial RVs
- Algorithm for Computing Median
- Chernoff Bounds (maybe Tuesday)
Chebyshev's Inequality
Proof:
- Just use Markov's Inequality:
- Define helper RV
Bernoulli Random Variables
- Example: Fair coin flip is Bernoulli RV with parameter . Indicator RVs!
General Properties:
- Expectation:
- Variance calculated similarly as for fair coin flip:
Binomial Random Variables
General Properties:
- Computing expectation and variance is straightforward!
Fast Computation of the Median
- We're given some unsorted data set: list of integers
- Median is the value separating the higher half from the lower half of the data set
- is median, if...
- at least elements are , and
- at least elements are .
- Goal: Output the median element in time (in RAM model)
- median:
- Easy way to compute median in time ?
- Sort list and output middle element in sorted order
Why the median is important
- Consider sample of household incomes
- Let's assume all except 1 sample earn .
- One sample earns 158.2 billion USD (e.g. CEO of Amazon.com)
- Value of Mean?
- Value of Median?
- Median is more robust to outliers!
Randomized Algorithm for Median - High Level
- Input: List of integers; odd
- Output: median of , i.e.: -th element in sorted order of
- Sampling of small subsets
- ...and sorting of small subsets
Main Idea:
Randomized Algorithm for Computing Median
Input: Unsorted array of integers;
Output: median of
- Sample elements u.a.r from . Store them in array .
- if or then: output fail and terminate
- if then: output fail and terminate
- output
Find and such that:
Proof:
Time Complexity:
- Sorting takes .
- Computing , , , takes , i.e., each time pass through .
- Sorting takes .
- time in total.
Correctness:
- Algorithm is correct if it either outputs fail or median.
- Suppose algorithm outputs . Is median?
- We know ; otherwise algorithm would have output fail
- (this is only element that is output)
- Exactly elements less or equal than
- doesn't contain smallest elements of
- element at position of is median of .
Analysis of Success Probability
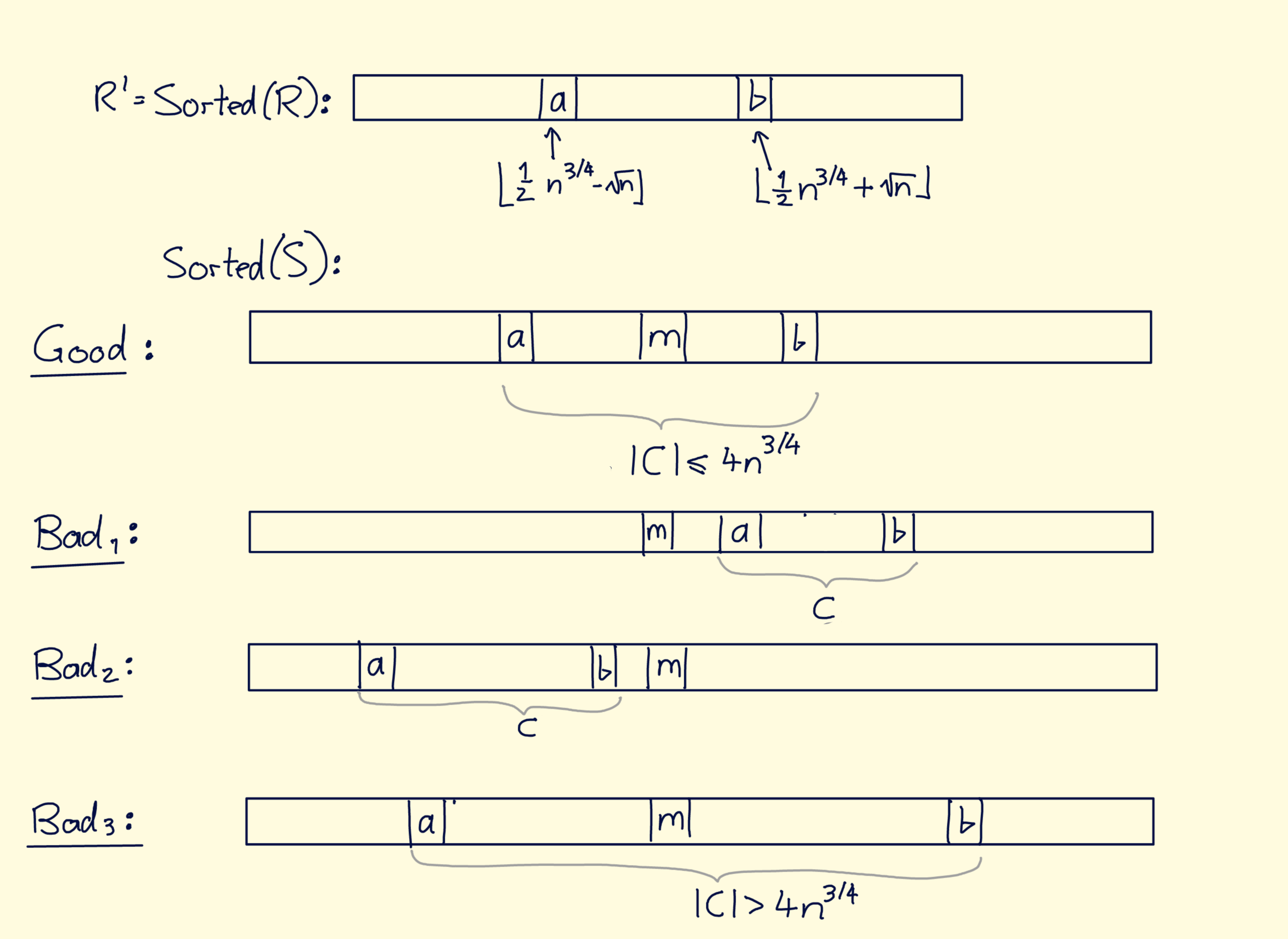
- : occurs if
- : occurs if
- : occurs if
Proof:
- occurs...
- because cannot be greater than ) smallest elements of
- Define
- Define
- Idea: Use Chebyshev's Inequality!
- First determine and ...
- Since :
- Now let's apply Chebyshev's Inequality:
Proof:
- Same analysis as for .
Proof:
- Define 2 events:
- Event : at least elements of are
- Event : at least elements of are
- If , then at least one of or occurs.
- Focus on event : at least elements of are . (Argument for is symmetric.)
- Recall that for all .
- event implies that position of in is
- Define
- Define . Then
- Define . Then and thus:
- Let's apply Chebyshev's Inequality:
- Recall that event happens if event or
- So far, we've shown that .
- Symmetric argument shows that .
- .
Combining All the Pieces
- Algorithm outputs median unless or or happen.
Can we make this a Las Vegas algorithm?
Interlude: Probability vs Logical Implications
- Consider events and .
- "" implies .
- Why?
- Recall: an event is set of outcomes
- So really means, for all outcomes , also
- Thus
- Probability of set cannot be smaller than probability of set .
- Example: , so
Chernoff Bounds
- Tail inequality for random variables
- Gives much tighter bounds than Markov's or Chebyshev's Ineq.
- Extremely common tool when analyzing stochastic processes and algorithms
General Version of Chernoff Bound
For any : For any :
Simplified Version of Chernoff Bound
For any :
Example: Concentration Bounds for Coin Flips
- fair coins, i.e., . Define .
- We already know , .
What's the probability of seeing more than heads?
- Not very useful here...
- We got a tighter bound, but we can still do better!
- Decreases exponentially in ! Very unlikely event.
Can we get even closer to the mean?
- , so .
- Choose
- Observing heads is unlikely for any constant !
Revisiting Randomized Quicksort
qsort(array):
if length(array) ≤ 1 then
return array
else
pivot = array[random(0..length(array))]
less_or_eq = [ x <- array | x ≤ pivot ]
greater = [ x <- array | x > pivot ]
qsort(less_or_eq) ++ [pivot] ++ qsort(greater)Proof:
- View execution of quicksort as binary tree:
- Root of tree is initial data set
- Left child is subproblem of sorting elements smaller than pivot
- Right child is subproblem of sorting elements greater than pivot
- Each internal node of tree is subproblem of smaller size
- Each leaf corresponds to singleton set
- Node of tree is good if subproblem of both children is at most of 's problem size.
- 2 Simple Properties:
- Number of good nodes in any path from root to leaf is at most .
- Consider sorted order of integers at some node .
- Good node reduces problem size by -fraction.
- If path contains good nodes, then...
- problem size
- problem size of for .
- Consider a path of length .
- Define indicator RV iff -th node in is good
- Define . Then .
- We've shown:
- We've shown:
- Take union bound over all paths:
- No path has length .
Application: Sampling & Polling
"What fraction of CAS alumni like Haskell?"
- Suppose we have samples from the population of CAS alumni.
- -fraction of CAS alumni like Haskell, where is unknown
- Its impossible to find exactly, so let's try to find "likely range":
- Goal: To have "confidence" , we need interval such that
- We want to be as small as possible!
- Let be # of sampled alumni that like Haskell.
- Then , for some . Important: likely that !
- Also: and .
- If then either:
- , hence
- , hence
- We want , so we set:
- If we fix and , how many samples do we need to get -confidence interval of size ?
Final Projects
- When designing new randomized algorithm, there's interplay between theory and experiment.
- From theory, we get insights what might work in practice
- From experiments, we can see what we should try to prove
- Goal of final project: To perform experiments with randomized algorithms.
Project Topics
- 3 topics: choose one to work on
- You can also suggest a different topic if it is related to the course.
- Write a report on your findings.
- Give a brief presentation in class.
Topic 1: Quicksort with Multiple Pivots
- Standard randomized quicksort uses pivot element at each recursive step to split elements into 2 smaller sets.
- In 2009, researchers obtained faster results using two pivots that split elements into 3 smaller sets.
- Implement (standard) randomized Quicksort and multi-pivot Quicksort.
- Perform baseline performance measurements (count number of comparisons!).
- How many pivots is optimal?
- What about parallelizing your implementation?
- How does the running time of your implementation scale with ?
- Try to use different data sets: almost pre-sorted,
Topic 2: Skip Lists vs Binary Search Trees
- Skip lists are an interesting alternative to binary search trees.
- Goal is to understand performance of skip lists compared to other (randomized or deterministic) data structures.
- Implement skip lists, treaps, and red-black trees.
- Perform baseline performance measurements.
- Which data structures perform best for which sequence of operations? Why?
- Use variety of data sets!
Topic 3: Contention Resolution
- One of the most frequent uses of randomization in real world
- Scenario: collection of devices/processes want to access some resource
- Resource can only be accessed by one user at a time (e.g. collision resolution in 802.11 WiFi)
- Assume that time proceeds in synchronous steps .
- In each step, a device can attempt to claim the resource.
- If it succeeds, then it completes. Otherwise, it backs off and tries again later.
- Backoff protocol determines time-window for retry.
- Goal: Experiment with Backoff Protocols
- Many variants: Linear backoff, exponential backoff, log-backoff, etc.
- Implement simple simulator that can run different backoff protocols
- Which backoff protocol works best? Under what circumstances?
Skip Lists
Geometric Random Variables
Properties
- Memoryless: Past failures do not change distribution of number of trials until first success.
The Memoryless Property
Proof:
Expectation of Nonnegative Random Variable
Proof:
Expectation of Geometric Random Variable
Proof:
- Let's use .
- So far: .
The Data Structuring Problem
- Given collection of data items:
- Each item has unique key
- Goal: Maintain keys of in a way that supports insert, search, delete in time .
- Standard Solution: represent keys in binary search tree.
Example
KeysDeterministic Binary Search Trees
- Deterministic solution to data structuring problem
- time operations if tree is balanced:
Performance is proportional to height of tree!
- Worst-case insertion sequences requires rebalancing of tree.
Example: Red-Black Tree
- Most popular self-balancing binary tree
- Each node has color: either red or black.
- Red nodes have only black children
- All paths from a node to leaf have same number of black nodes
Rebalancing Red-Black Tree
- Maintaining invariants requires rotations
- Might affect large parts of the tree: problematic when data is partitioned across several machines
- Implementing concurrent write-access to elements is tricky
Deterministic Variant of Skip Lists
One-Shot Construction
- Consider ordered collection of keys .
- Build level linked list .
- Build level linked list
- Add double pointers between identical elements in and .
- Build level linked list by omitting every second key from ; add double pointers between identical elements
- Elements in hold reference to stored items of respective keys.
- is called top list
- We get distinct linked lists .
Example: Skip List of keys
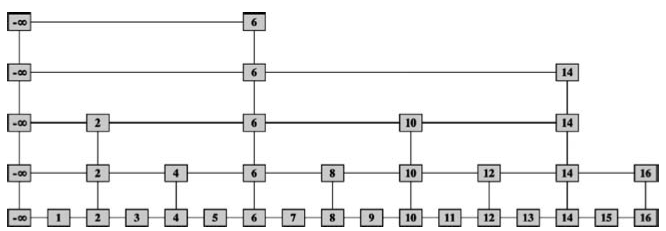
Searching in Skip Lists
Suppose we search for key :
- Start at left-most element in top list .
- Scan right until we hit largest element where
- Move one level down to identical copy of in list
- Scan right until we hit largest element where
- ...and so forth until we reach
Remarks:
- Search generates sequence .
- is found if and only if
- Zigzag traversal: We only make downturns and right turns.
Performance:
- How many pointers do we need to follow?
- Depends on number of right turns and downturns!
- How many downturns? There are lists.
- How many right turns? Each right turn roughly halves search space, so
Randomized Skip Lists
- As before: skip list is collection of linked lists
Search for key :
- Implementing Search:
Same as for Deterministic Skip lists - start at top-left and traverse zigzag-style
Construction - one element at a time:
Suppose we want to insert key :
- Insert between and its successor in
- for do:
- if outcome of fair coin flip is...
- 3.1. tails: break for-loop
- 3.2. heads: insert between and its successor in
- Number of times we get heads until first tails determines height of element.
Deletion:
Suppose we want to delete key :
- if is in skip list then: .
- For each identical copy of : remove from linked list ; use "up" pointers!
Skip Lists - Performance
- For both, insertion and deletion:
- First search
- Then perform 1 operation per level
- Performance of insertion & deletion depends on search and height of skip list, i.e., number of levels!
Height of a Skip List is logarithmic whp
Proof:
- For each , define height to be highest level on which .
- follows geometric distribution with parameter
- We've shown that, an element has height whp:
- .
- Taking a union bound over elements:
Performance of Search
- Search traverses skip list in zigzag-manner starting at top-left.
- Let RV be number of downturns.
- Let RV be number of right turns.
- Then RV is number of arrows in search traversal.
Proof:
- We already know that :
- Let's use events and to partition sample space of and apply Law of Total Probability:
Proof:
- Suppose we search for , and traverse a right turn "" in some list .
- Then element must have height :
- Assume in contradiction that has height , i.e., .
- We only traverse "" if .
- But then we should have also visited on higher leve, i.e., when traversing (recall: we never go left!)
- Contradiction!
- Since has height , it got "tails": happens with prob. .
- Consider search path length of , i.e. .
- .
Combining the Pieces
We've shown:
- It follows:
- With high probability, a search doesn't traverse more than right/down arrows.
- Insertion and deletion also take time.
Skip Lists - Summary
- Skip lists are used in real-world databases (e.g. Redis)
- No rebalancing required
- Great for implementing parallel write-access to elements
Proof of Chernoff Bound
For any :
Proof:
- Let . For any :
- What's ?
- Back to showing the bound...
- So far, we just assumed . Now plug in :
For any :
- How do we derive the simpler version from more general one?
For any :
For any :
- We need to show:
- Taking logarithms on both sides, equivalent condition is:
- Treat as and compute , .
- Can be checked to be true using derivative test.
More Convenient Chernoff Bound
Let .